Un exemple, un test et une définition
Prenons un exemple simple pour ce tutoriel : disons que vous souhaitez savoir si une pièce de monnaie est biaisée. Pour le vérifier, vous décidez de la lancer 20 fois, et de compter combien de fois « face » apparaît.
Si votre pièce est parfaitement équilibrée (c’est-à-dire qu’elle a 50 % de chances de tomber sur « face »), le nombre attendu de « face » sur 20 lancers serait de 10. Toutefois, il est peu probable d’obtenir exactement 10 faces (avec une pièce équilibrée, cela a environ 17 % de chances d’arriver). Alors, comment savoir si un résultat sort de la norme ?
Imaginons que vous testiez une pièce, et que vous obteniez 15 fois « face ».
La p-value de ce test correspond à la probabilité qu’une pièce parfaitement équilibrée, lancée 20 fois, donne un résultat aussi égale ou plus à 15. Si l’on regarde la distribution des résultats attendus, cette probabilité est représentée par la portion de la courbe colorée en bleu, qui vaut ici environ 0,041. Obtenir moins de 5 ou plus de 15 faces correspond à la limite de p < 0,05.
(illustration : distribution de probabilité – pile ou face)
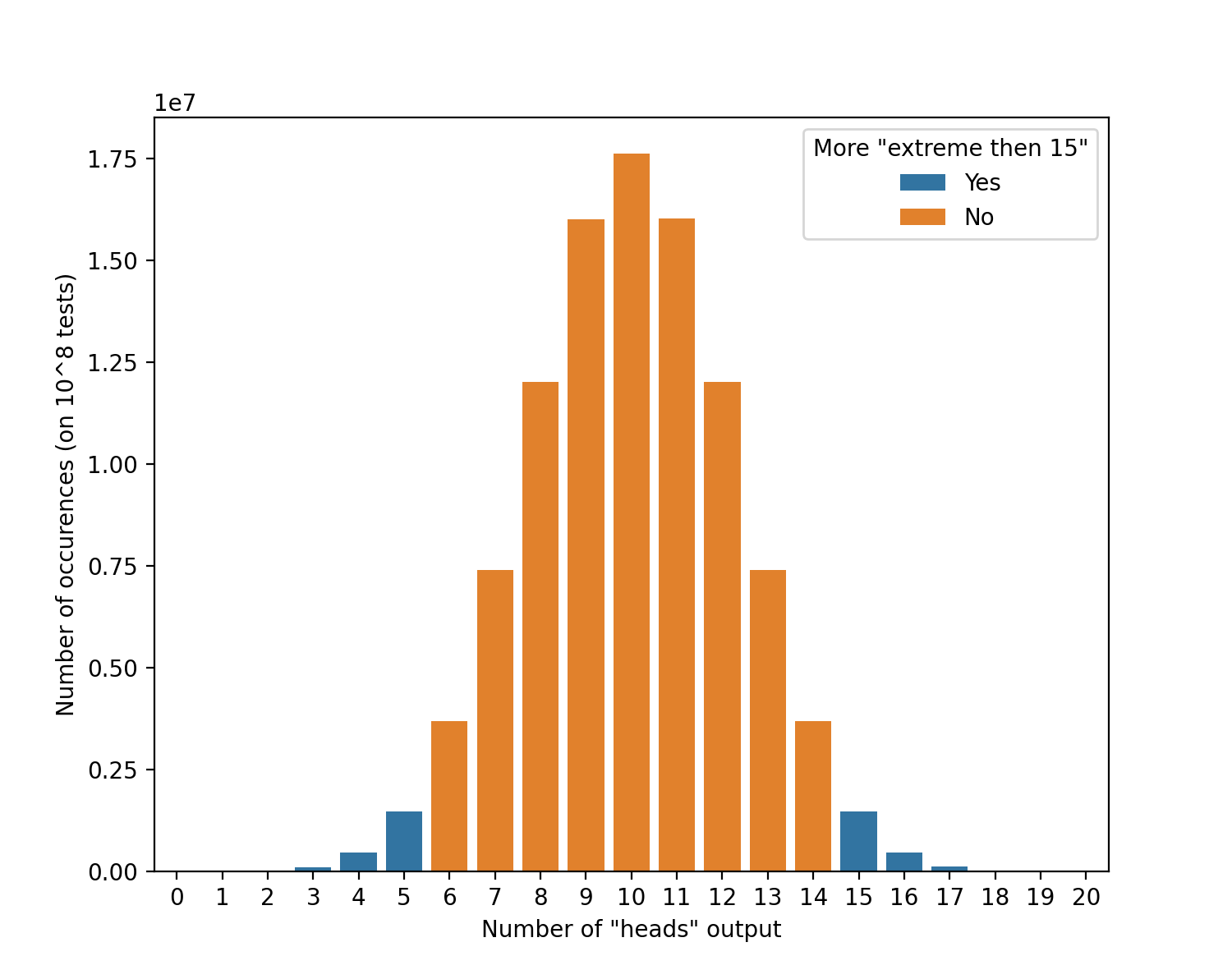
Maintenant que vous avez une idée générale du concept, allons un peu plus loin.
Une définition plus formelle de la p-value
L’hypothèse nulle
Pour calculer une p-value, il faut définir ce que l’on appelle une hypothèse nulle (ou H₀), qui correspond à ce que l’on attendrait dans des circonstances normales. Dans notre exemple :
> H₀: une pièce parfaitement équilibrée tombe sur « face » 50% du temps.
Dans la majorité des cas en bioinformatique, cela correspond à : “la biologie suit exactement le modèle attendu”, “ces éléments biologiques n’interagissent pas entre eux”, ou une variante de ce type.
Le test
Il faut ensuite définir un test T, à l’avance: dans notre cas “Compter le nombre de fois où l’on obtient « face » sur 20 lancers”
Si vous appliquez ce test à une pièce données et que vous obtenez un résultat R, la p-value correspondante est “la probabilité d’observer un résultat similaire ou plus extrême dans un cas où H₀, est vraie”.
Comment une p-value est-elle calculée en pratique ?
S’il s’agit d’un test classique, déjà implémenté dans les outils statistiques, ces derniers vous fourniront automatiquement une p-value. En pratique, ils utilisent des modèles mathématiques pour représenter les résultats attendus sous H₀. Ces modèles définissent eux-mêmes H0,, donc idéalement, vous devez vous assurer qu’ils sont adaptés à votre problème.
Par exemple, la formule mathématique permettant de calculer la p-value mentionnée plus haut serait
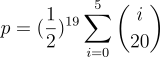
…en supposant bien sûr qu’une pièce ne tombe jamais sur la tranche.
Dans des cas plus atypiques, où aucun test statistique standard n’existe, vous pouvez avoir recours à des simulations informatiques. Il s’agit alors de lancer virtuellement des centaines de milliers de pièces parfaitement équilibrées, et de compter combien de fois vous obtenez un résultat aussi extrême ou plus extrême que celui observé. Vous n’obtenez alors qu’une estimation de la p-value, mais cette approche permet de modéliser des situations plus inhabituelles, par exemple, une pièce ayant une chance sur 1000 de tomber sur la tranche. Cela nécessiterait toutefois un peu de programmation de votre part.
Dans ce cas, votre p-value estimée serait :
In fact if you look in detail to the above curve, you can see that it’s been created using a simulation.
Que signifie réellement une p-value, et à quoi correspond le seuil de 5% ?
Alors, que signifie exactement une p-value inférieure à 5 % ?
Cela indique que le résultat observé est peu probable (moins de 5 % de chances) dans une situation où H₀ est supposée vraie.
Et cela s’arrête là!
Le seuil de 5 % est une convention, sans signification absolue. Il s’agit d’un seuil arbitraire. L’idée générale est que plus votre p-value est faible, moins il est probable que vous détectiez un effet inhabituel alors qu’il n’y en a pas.
Mais attention : une p-value faible suggère que H₀ est peu probable, ce qui ne signifie pas que votre hypothèse personnelle est correcte. Un autre facteur non pris en compte peut tout aussi bien expliquer le résultat.
À l’inverse, une p-value supérieure à 5 % ne signifie pas qu’il ne se passe rien, mais simplement que les résultats de ce test, dans ces conditions précises, ne contredisent pas H₀. Nous approfondirons cela dans un prochain tutoriel dédié à la puissance statistique.
À lire aussi

Tests multiples et correction de la p-value
Vous avez peut-être déjà entendu parler de ces termes, ou peut-être pas, chacun suit son propre chemin. Mais comme il s'agit de concepts essentiels pour comprendre et utiliser les p-values, j'espère que ce tutoriel vous sera utile, qu'il s'agisse d'une remise à niveau...

Manuel d’introduction au cluster iPOP-UP : connexion, Slurm et bonnes pratiques
Lien vers la documentation sur l’utilisation de la ressource de calcul iPOP-UP@RPBS.
