p-value : an introduction

An example, a test and a definition

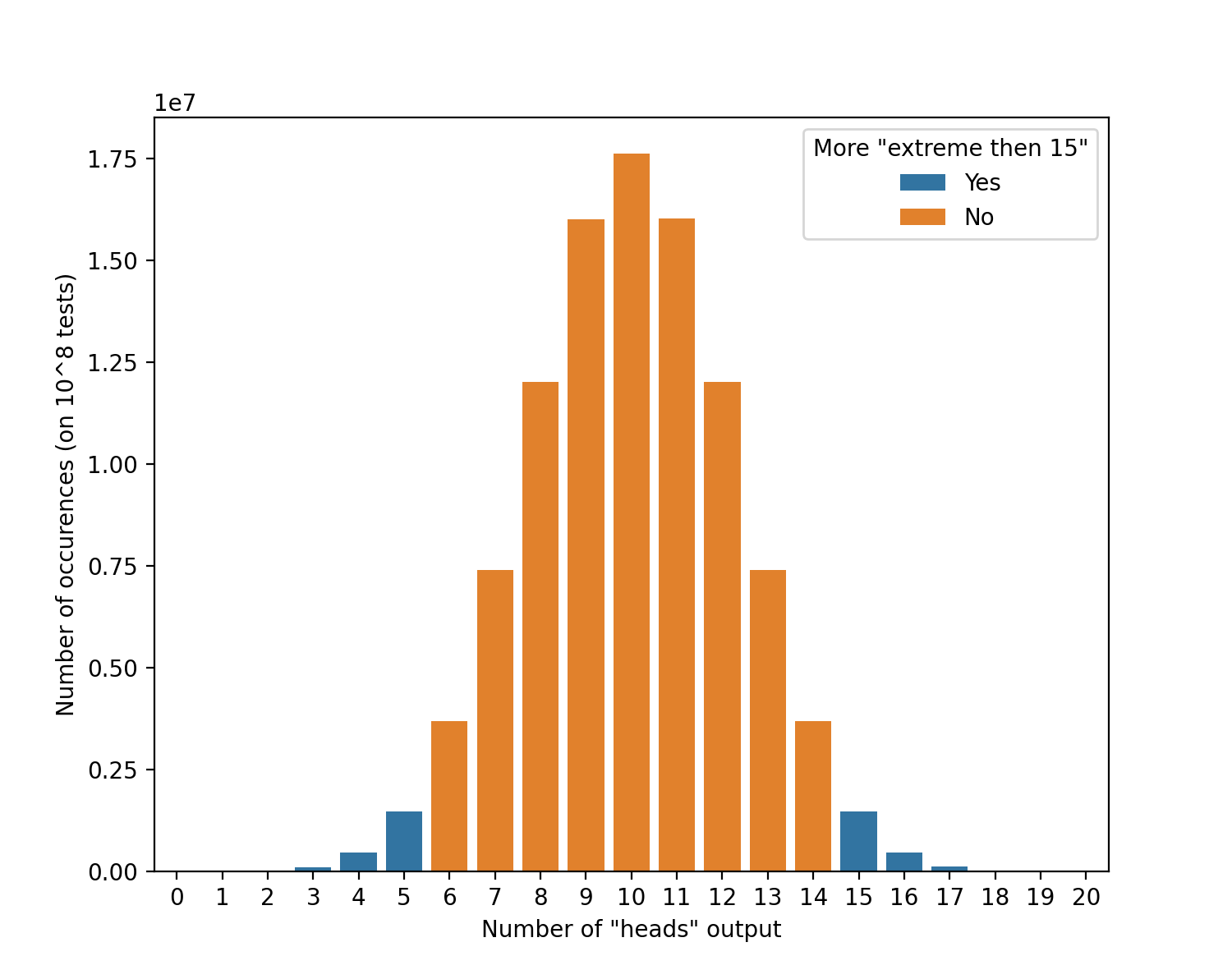
Let’s pick a toy example for this tutorial, let’s say you want to know wether a specific coin is biased. In order to test it, you decide to flip the coin 20 time, and count the number of times “head” comes out.

If your coin is perfectly balanced (meaning in this case, it has 50% chance to come out on head), the expected number of head you would obtain for 20 throw would be 10. However, you are not very likely to see “heads” exactly 10 times (in fact with a balanced coin, this has a probability of around 17% to happen), then how do you test wether a result is out of the norm?

Let’s assume that you test a specific coin, and that the results that you obtain “heads” 15 times.

The p-value of this test is the probability for a perfectly balanced coin, when thrown 20 times to have a results equal or more extreme than 15. If we look at the distribution of expected results, it is represented by the proportion of the area colored in blue, which: in this case is round 0.041. In fact, Less then 5 or more than 15 heads in our test correspond the limit of p<0.05.

Now that you have the general idea of it, let’s get more precise.

A more formal way to describe the p-value

The null hypothesis

To compute a p-value, we need what we call a Hypothesis Zero (or H0), this corresponds to what would be expected under normal circumstances. In our coin testing example this was.

> H0: a perfectly balanced coin falls 50% of the time on head.

In most case in bioinformatic, this is “The biology corresponds exactly to what is expected”, “those biological elements do not interact with each other” or some variant there of.

The test

You need a specific test T, defined in advance: in our case “Count the number of head when thrown 20 times”

If you do the test on a specific coin and obtain results R, the corresponding p-value of R would be “the probability of seeing a results similar or more extreme in a case where H0 is true”.

How is a p-value computed in practice

If it is a classical test, the kind which is already implemented. The tool you’re using will most likely give you a p-value by itself. In practice they used some mathematical models to represent the expected results in H0. Those mathematical models are in themselves defining H0, so ideally, you should make sure that it actually fits your problem.

For example, the mathematical formula for the p-value computed above would be

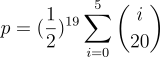
… assuming of course that a coin never falls on its edge

In more exotic cases, where a test doesn’t exist you can resort to informatics simulations. Digitally throw hundred of thousands of perfectly balanced coins and count the number of time you obtain a result equal or more extreme than what you have. You only have an estimation of the p-value, but you can model more exotic results, such as the coin having a 1/1000 chance to land on it’s edge, but it would require some coding on your part.

In this case, your estimated p-value would be

In fact if you look in detail to the above curve, you can see that it’s been created using a simulation.

What does the p-value actually means, and the 5% threshold

With all of that being said, what does having a p-value under the 5% actually means?

It means that your results are unlikely (less than 5% likely in fact) to be observed in a case where H0 is true.

And that’s pretty much it!

The 5% threshold is a convention, but does not have any specific meaning, it is an arbitrary threshold. The idea is, that the lower your p-value is, the less chance you have of saying that there is something weird when there is nothing out of the ordinary.

Most importantly, a low p-value does indicate that we are unlikely to be in the case where H0 is true, but it doesn’t validate your personal theory. Most importantly, another phenomena that you didn’t consider might be causing the results.

And finally, a p-value above 5% does not mean either that nothing is going on, just that the results of this specific test, this specific time are not abherent in regard to H0. We will discuss this more in details when talking about statistical power, in its own tutorial.